上一篇讲到，现在我们还有两个问题，第一，为什么上一步减少get_vec_element的优化，看起来没有作用。第二，combine4是否还有进一步优化的空间。

要回答这两个问题，我们需要先稍微了解一下现代处理器的一些内部操作流程。

前面都是些基本的优化操作：

• 降低循环的低效率
• 减少函数调用
• 消除存储器引用，使用临时变量

这几个方法都是处理器无关的，不依赖任何机器特性。接下来，就要利用处理器的一些处理方式来有正对性的优化了。

从汇编级来看，指令都是一条条执行，每条指令都包括从寄存器或者存储器取值，执行一个操作，并把结果放回寄存器或者存储器。但在实际的处理器中，是同时对多条指令求值的，这个现象称为指令级并行，在某些设计中，可以有100或更多的指令在处理中。当然，处理器会有很多精细的机制来保证，指令看起来是简单的顺序执行的。

似乎进入了魔法领域

下图是基于近期Intel处理器的一个近似结构，它的一个特性叫做超标量，意思是它可以在每个时钟周期执行多个操作，而且是乱序的，即可能跟他们在机器级代码中的循序不一致。整个设计有两个主要部分ICU(Instuction Control Unit 指令控制单元)和EU(Execution Unit 执行单元)。

听到ICU是不是觉得虎躯一震。。。

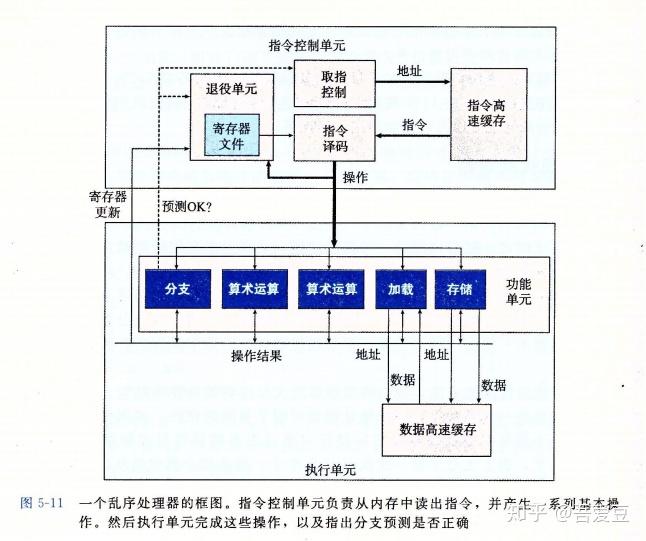
处理器在遇到分支跳转的时候，会采用一种分支预测的技术，用来投机提前执行一些操作。预测就有可能错误，当预测错误的时候，提前执行的东西就浪费了，需要重新取出另一个方向上的指令。

指令解码将汇编指令转换成一组基本操作。例如addl %eax,%edx 产生一个加法操作，而addl %eax,8(%edx)则会产生三个操作——加载内存，加法操作，存回内存。

如图5.11中，有一个退役单元, 这个部分记录正在进行的操作。一旦一条指令操作完成了，而且所有引起这条指令的分支点也都被确认为预测正确，那么这条指令就可以退役了，所有对程序寄存器的更新都可以被实际执行了。反之，如果预测错误，则指令被清空，计算出的结果被抛弃。

任何对程序寄存器的更新都只会在指令退役的时候才会发生。

所谓寄存器重命名就是一种减少寄存器读写等待的技术，一个要写寄存器的操作，可能因为是在预测分支中，无法直接写入，需要等待后续确认之后才能写入，那么该分支上后续指令需要使用这个寄存器，那么就在一张特定的表中取查询该值，从而跳过等待。即使没有分支预测，也能加快指令的执行，无需等待写入。

这个设计可以考虑怎么利用到项目中，对于那些更新数据会引起一连串变化的操作，可以进行数据缓存，把实际的更新延后。而取数据的时候需要先检测缓存。

下标是Intel Core i7参考机的一些算术性能。这里的容量是表示该运算的功能单元的数量。这个数量也是处理器能同时处理多个相同操作的基础。

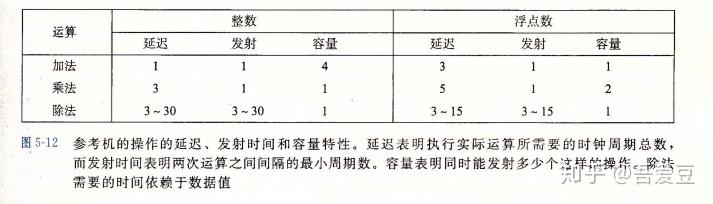
加法和乘法的发射时间都是1，这是通过流水线来实现的。当个操作没有结束就可以开始新的阶段操作。

除法运算时没有流水线实现的，它的发射时间等于延迟，说明新的运算需要等上一个运算结束后才开始。所以除法很慢。

功能单元的最大吞吐量为发射时间的倒数。容量可以增加吞吐量，例如容量为C，发射时间为I ，则吞吐量为 C / I 。而下文提到的吞吐量界限则是吞吐量的CPE表示，即吞吐量的倒数。例如吞吐量为2，表示每个时钟周期能执行两个操作，即相应的CPE为0.5 。

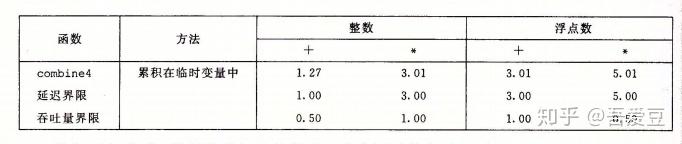
前面combine4函数目前为止是最快的，这里对比下该函数与理论值的比较：可以看到距离理论值还有一定的距离，我们能达到理论值吗

combine4循环的汇编代码如下：

其操作对寄存器使用如下：

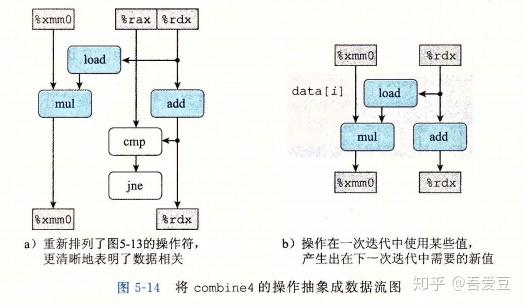
从这个图上，就能够看得出来，mul操作跟load，add操作是并行的。从上面的表格可以看到combine4浮点数的延迟为5.01，而浮点的mul的延迟正是5.0，这就是说mul是整个瓶颈，其他操作都是和mul并行执行的。

并行！指令集的并行，一些并不互相依赖的操作是可以并行执行的，占用的时间也就忽略不计了。这就解释了前面的第一个问题，为什么优化了一个函数调用居然没有效果，就是因为之前内存的访问是瓶颈，其他的操作在内存访问的同时可能就完成了。

下面的习题示例很有意思：一个明明看起来操作变少了的算法，实际执行实际却更慢，先来看题目，要求计算多项式值 ,有以下方法

// 1.传统方法
double poly(double a[], double x, long degree) {
    long i;
    double result = a[0];
    double xpwr = x;
    for (i = 1; i <- degree; i++) {
        result += a[i] * xpwr;
        xpwr = x * xpwr;
    }
    return result;
}

// 2. 采用Horner法，减少乘法数量，反复提出x的幂, 即 a0 + x(a1 + x(a2 + ... ))
double poly2(double a[], double x, long degree) {
    long i;
    double result = a[degree];
    for (i = degree - 1; i >=0; i--) {
        result = a[i] + x * result;
    }
    return result;
}

第一个方法需要的加法为degree次，乘法则是2*degree次。而第二个方法乘法变为degree次，足足减少了一倍。然而实际测试中，方法一的CPE为5.0，而方法二的CPE为8.0。

这是因为方法一种两个乘法操作实际上可以并行操作，瓶颈实际上是xpwr=x * xpwr;。在此操作期间上面的加法并行的执行完成了。而方法二中的乘法计算要依赖result，没法实现并行运算，需要算完乘法，再算加法，更新寄存器，然后才能开始下次循环。

自己想了一下，还是没有想懂。方法一第七行的加法，本身也是要依赖a[i]* xpwr的，这个乘法本身就需要5个周期，然后计算加法，更新寄存器。下一次循环，也是要等这个result更新完毕才能开始的吧？ 如果这样的话，那么也是需要8个周期才对啊。如果少于这个，难道说7行的乘法结束后，就可以开始下次循环了？
强行自我解释：第7行的乘法不依赖result，乘法开始的同时，第8行立刻就开始了。第8行开始之后，就开始进行下一次循环的第7行，这个时候等待第一个第8行的操作结束，一旦结束，立刻又开始新的第8行。简而言之，第一种写法的时间从常用来看只跟第8行有关。第7行还有个 result+=难道这个不消耗的吗？消耗，不过呢，它可以在下一个第7行乘法开始的时候，再计算上一个result的加法，因为大家互相都不依赖。计算都是重叠的。
这就是指令集并行的威力。

前面简单介绍了什么叫循环展开，这一节正式的介绍如何使用循环展开来优化。

循环展开即增加每次迭代计算元素的数量，从而减少迭代的次数。循环展开从下面两方面改进性能：

• 减少操作数量，例如计算索引和条件判断
• 提供了后续进一步优化代码的空间以便减少关键路径上操作的数量。

// 对combine4做2*1的循环展开
void combine5(ver_ptr v, data_t *dest) {
    ...
    long limit = length - 1;
    for (i = 0; i < limit; i+=2) {
        acc = (acc OP data[i]) OP data[i+1];   // 一次循环实际计算了两个元素
    } 
    for (; i < length; i++) {
        acc = acc OP data[i];
    }
}

对于展开次数k，上限limit应当设置为length - k + 1 ，并且后续需要增加循环 for(; i < length; i++)来处理尾部剩下的数值。

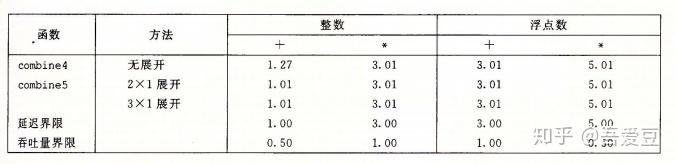
可以看到，展开之后，只有整数加法提供了效率，其他部分因为已经达到延迟的界限，没有任何改变。观察下图中操作的关键路径可以看出，跟之前的单循环差别不大，减少了add的次数而已。

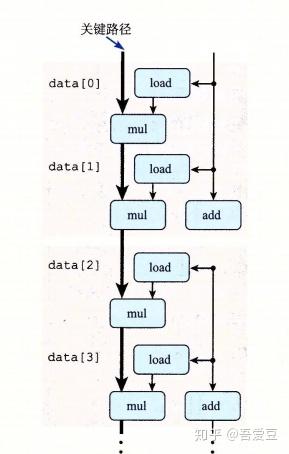
现在到了关键的时候了，到达延迟界限之后，还可以继续提供性能吗？能够突破延迟界限，到达吞吐量界限吗？让我们拭目以待吧，是时候展现真正的技术了。

加法和乘法是完全流水线化的，这说明每个时钟周期都可以开始一个新的操作，即使前面的计算没有完成。而前面的循环展开没法使用这种能力，是因为每次计算的结果在同一个变量当中，下次循环需要等待上次的结果。基于这个情况就引出了新的优化方法：使用多个累积变量

简单来说就是，将前面函数的acc拆成两个变量，各算各的，最终再汇总。上代码。

void combine6(vec_ptr v, data_t *dest) {
    long i;
    long limit = length - 1;
    long length = vec_length(v);
    data_t *data = get_vec_start(v);
    data_t acc0 = IDENT;
    data_t acc1 = IDENT;
    for (i = 0; i < limit; i+=2) {
        acc0 = acc0 OP data[i];   // 分别计算各自的内容
        acc1 = acc1 OP data[i+1];
    }
    for (; i < length; ++i) {
        acc0 = acc0 OP data[i];
    }
    *dest = acc0 OP acc1;
}

令人震惊的事情发生了，conbine6的性能突破了延迟界限！除了整数加法，其他操作提高了2倍！

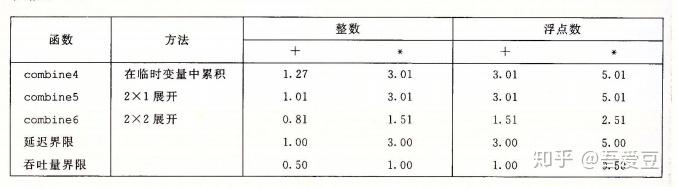
之前计算吞吐量界限的时候，它的计算是，延迟 / 模块的容量，这意味着，必须要并行的使用多个计算模块，才有可能逼近吞吐量界限。现在已经突破延迟，说明并行已经起作用了。

再来看2*2展开的操作图，对比之前的图，可以看出来，第二个load和mul都不需要等待前面的操作结束，直接开启了新的流水线。

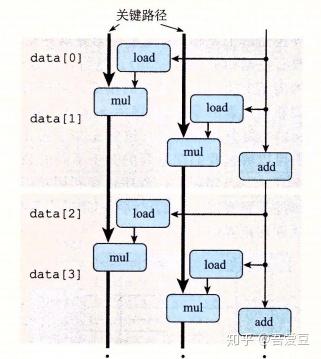
当某类计算的相关所有功能单元的流水线都是满的时候，程序就能接近达到吞吐量的界限。对于延迟为L，容量为C的操作来说，循环展开因子k >=C * L时可以达到最大性能。例如浮点乘法 C为2，L为5，则展开因子k>=10 。浮点加法C为1， L为3，则k>=3时获得最大性能。（图5-12展示了i7处理器各操作的容量和延迟）

需要注意的是，浮点数的乘法和加法实际上不满足结合律的，所以对于特定的数值combine5和combine6的结果会存在完全不同的结果。

另一种打破延迟极限的方法，更加的让人匪夷所思，对combine5稍作修改如下：

for (i = 0; i < limit; i+=2) {
    acc = (acc OP data[i]) OP data[i+1];   // 一次循环实际计算了两个元素
}
// 改为
for (i = 0; i < limit; i+=2) {
    acc = acc OP (data[i] OP data[i+1]);   // 一次循环实际计算了两个元素
}

仅仅是先计算后面两个项，再计算与acc的和，结果是：

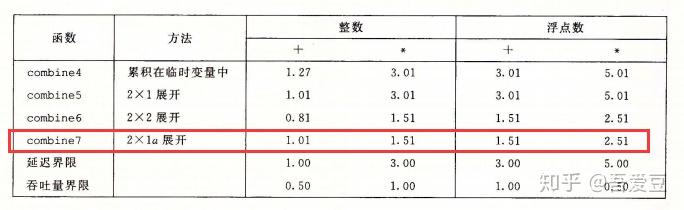
这个改动在浮点数上，已经跟combine6使用多个累积变量效果一致了。这是为什么呢？

上面的改动，实际上等价于 acc +=data[i]+ data[i+1]或者 acc *=data[i]* data[i+1]，这说明使用 +=*=是个好习惯，在自己不知道的情况下优化了计算。

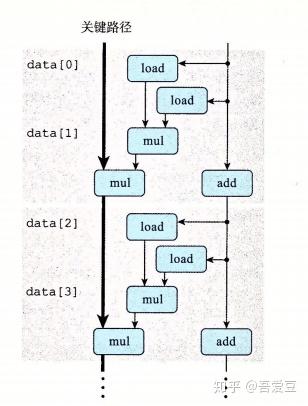
从操作流程图上来看，也依旧充分的利用了流水线的特性。就是说第一次迭代开始计算acc * 临时结果这个乘法的时候，下一次迭代的data[2]* data[3]就可以开始了，因为这个乘法不依赖acc，不需要等acc乘法的结果。

看到这里，应该能够明白前面那个计算多项式的习题中，第7行result +=a[i]* xpwr; 为什么比较快了吧。

重新结合变换能够减少关键路径上的操作数量，能够更好的利用功能单元的流水线能力。编译器有时候会做一些整数运算的重新结合，但是效果并不是特别好，而使用累积多个变量是更可靠更稳定的方法。

SIMD可以使用一条指令对整个向量的数据进行操作，目前AVX的寄存器长为32字节，256位，即可以对8个32数或者4个64位数并行操作。该方法也能极大的提高一些频繁操作的数据的效率。

可以参考 SIMD简介

先来看看从combine1到combine6的性能对比：

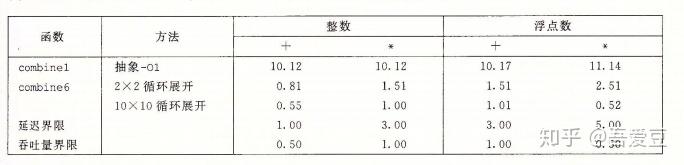
以整数加法为例，从10.12的CPE，到0.55的CPE，基本逼近0.5的理论极限。几乎提升了20倍，如果使用SIMD重写，可以再获得4到8倍的提升，例如浮点数乘法的CPE能够降到惊人的0.06 。不过啊SIMD写法看起来比较复杂，可读性不强，只有那些极其需要性能的地方才用吧。

循环展开也不是可以随意数量的无限展开的，例如寄存器数量只有16个，展开数量超过16个肯定是寄存器溢出的，溢出就只能存到栈上，可能反而会降低效率。

这叫什么，过犹不及啊

前面提到过，处理器在遇到分支的时候，会直接投机的提前执行其中一个分支。这种预测如果错误，就需要丢弃掉所有的执行结果，从正确的位置重新开始取指令过程，错误处罚也就是这个地方引起的，因为指令流水线需要重新填充。

新的x86处理器增加了条件传送指令，可以用于减少分支预测。例如int a=b ? c : d; 将可能使用条件传送指令而不是跳转指令。

对于程序员而言，没什么简单的方法避免分支预测，但可以遵循下面两个原则：

1. 不要过分关心可预测的分支 处理器有很多有经验的预测方法，在一些规律模式上有很好的预测成功率
2. 书写适合用条件传送实现的代码 例如前面的 ? : 代码就能够直接翻译为选择传送。

注意，本节中的内存性能只考虑数据都放在高速缓存的情况。第6章会深入研究高速缓存是如何工作的，以及如何编写充分利用高速缓存的代码。

现代处理器有专门的功能单元执行加载和存储操作，这些单元内部会有缓冲区来保持未完成的内存操作请求集合。例如i7上，每个加载单元可以保持72个未完成的读请求，存储单元可以保持42个写请求。

要确定一台机器上的加载操作的延迟，这里设计了一个简单的代码，每次循环测试依赖加载的数据。

long list_len(list_ptr ls) {
    long len = 0;
    while (ls) {
        len++;
        ls = ls->next;
    }
    return len;
}

测试表明list_len的CPE为4.0，这个测试结果与参考机的L1级cache需要4周期的访问时间吻合。

读高速缓存速度都这么慢？寄存器呢？访问需要多长时间？
这也是前面消除存储引用优化中的原因了，访问存储器慢啊。

在大多数情况下，存储操作能够完全流水线化，也就是说没个时钟周期都可以发射一个新的存储指令。例如下面的代码可以达到CPE1.0，对于单个存储功能单元的机器，已经到达流水线的极限

void clear_array(long *dest, long n) {
    long i;
    for (i = 0; i < n; i++) 
        dest[i] = 0;
}

存储操作不会影响任何寄存器的值，因此，一系列存储操作不会产生数据相关，只有加载操作会受存储操作结果影响。

读写相关，会导致性能下降，因为要等待写入完成。而地址不同，则可以并行的执行，时间低的将忽略不计。例如下面的代码：

void write_read(long *src, long *dst, long n) {
    long cnt = n;
    long val = 0;
    while (cnt) {
        *dst = val;
        val = (*src) + 1;
        cnt--;
    }
}

当src和dst地址不同时，这段代码的CPE为1.3 ，而当两者地址相同时，CPE变成了7.3 。

存储单元包含一个存储缓冲区，它包含已经被发射到存储单元，而又没有完成实际存储操作的地址和数据。通过这种方式，使得存储操作不必要等到实际更新完内存之后才继续执行。而一个加载操作则需要先检测缓冲区是否有相同的地址，如果有则返回缓冲区的数据，而不是去内存中加载。

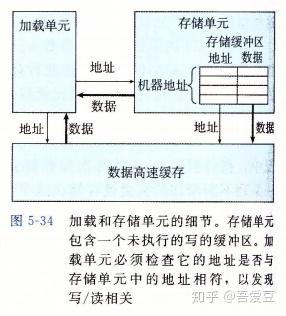
即便有了存储缓冲区，load和write相关的话，load则需要等待缓冲区写入完成才能执行，即load和write没法并行的执行。

流水线都无法开启？还是说写入存储缓冲区就得6个时钟周期？
例如第5行*dest=val; 如果后续没有读请求，写入可以每个周期发射一条指令，完全不用等待。这里不太能理解第7行，怎么也要加载src啊，val依赖src，下个循环要依赖val，则间接依赖src的加载。循环CPE为什么能到达CPE1.3这么高？除非说整个流程都流水线化了，寄存器的写入依赖可以通过寄存器别名之类的优化。从而完全并行的执行循环所有操作。

从下面的流程简化图，可以略窥一斑。

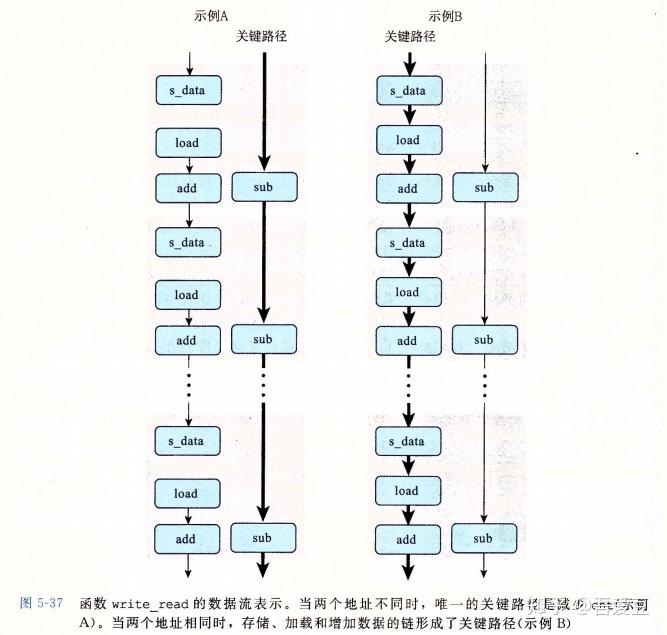
内存操作的实现包括许多细微之处，对于寄存器操作，在译码阶段，处理器就可以确定哪些指令会影响其他指令。而内存操作，则需要等加载和存储的实际地址计算出来之后，才能知道是否需要互相依赖。这种依赖会破坏并行，当加载和写入不是同一个地址时，则他们就可以并行的进行。

1. 高级设计 选择适当的算法和数据结构，避免指数级增加消耗的算法和编码技术
2. 基本编码原则：
3. 消除连续的函数调用。将可以移出循环的函数或者计算移出来
4. 消除不必要的内存引用。加载内存和写入内存都有消耗，使用中间变量来减少内存的访问
5. 低级优化
6. 循环展开，降低循环开销
7. 使用多个累积变量的方法，利用处理器指令并行处理能力
8. 使用功能性风格重写条件判断，减少判断，便于使用条件传送功能。

需要注意，优化代码不应该改变代码本身的逻辑，同样的输入应当产生同样的输出。

本章中，我们了解了一些基本的优化手段，并且知道了这些优化手段背后的原理，也知道了不同的优化手段的局限性。例如：

• 减少过程调用；减少循环中不必要的函数调用等
• 减少内存引用：读写内存依赖会破坏流水线
• 循环展开，多重展开：减少循环消耗，提供后续并行的基础
• 使用多个变量作为累积变量来提供指令并行：充分利用处理器的并行能力

我们也了解了现代处理器拥有多个操作模块，对加法和浮点数也都有不同数量的操作模块，这些模块能够并行的执行，从而实现指令级别的并行执行。有了这个基础，我们才能够针对性的对程序精心的改造，以让处理器更好的并行执行。

我们还了解了内存的一些性能限制，存储单元中存在存储缓冲区，可以使得写入指令不必完全完成，就可以开始下一个指令，从而实现流水线。所以单纯的读跟写都不会是性能瓶颈，而相互依赖的读跟写则会大大影响流水线的发挥。

看了不等于会用，这些优化手段乍一看好像很厉害，但是想快速的用到实际项目中却并非那么容易。为什么，除非恰好是一个数学类的计算，其他情况下各种循环中操作的内容都相当的复杂，各种函数调用。但是没有关系，学习的是一个方法论，培养自己的这种意识，慢慢的去想办法实践。